Last night, Jake Gardiner made a bad decision. Faced with a 2-on-1 in a tie game midway through the 2nd period, Gardiner made what seemed like the smart choice – he played the pass, leaving Curtis McElhinney to deal with what appeared to be an easy foe in 34-year old Trevor Daley[1]. Daley, however, defied the odds[2] and placed a perfect shot in the top left corner to give the Red Wings a 2-1 lead.
While defensemen are often taught to take the pass and leave the shooter to the goalie, Gardiner’s execution left a lot to be desired. As Justin Bourne noted, when you give the shooter that much space you’re basically turning a 2-on-1 into a 1-on-0.
Beyond the poor execution though, there’s a more general question about the wisdom of playing the pass and not the shot. Taking the pass and trusting your goalie to stop the shot is an idea that’s drilled into defencemen’s minds from a young age, and on its face it makes a lot of sense – we know that shots of passes go in more often than those off shots, so if you’re looking to minimize goals against (a pretty good idea for a defencemen) your best bet is to take away the higher percentage play.
The problem with this thinking though is that if you play the pass every time it will start to affect your opponent’s behaviour. Shooters will become more aggressive and work towards better shooting locations, which will start to eat away at some of the advantage from defending the pass. There’s a balance to be struck between preventing the more dangerous play and becoming too predictable. Playing the pass more often will probably always be the right play, the question is how often defenders should change things up and play the shot.
On the flip side of things, attackers face a similar decision when they choose whether to shoot or pass. A player with the puck on a 2-on-1 will obviously prefer to setup the higher percentage opportunity (or should prefer to a pass at least, I’ve certainly played with players who would shoot 100% of the time), but if they choose to pass every time they become easy to defend. We know that how each player acts will impact the other’s optimal decision, the question is whether we can predict how often each player will (or should) choose each action based on their incentives (expected goals).
This kind of problem makes it the perfect time for some game theory game theory. The decision of how often to pass/shoot or defend the pass/defend the shot is just a matter of finding the Nash equilibrium in a mixed strategy game. For each player, we want to find the percentage of the time they should pass (or defend the pass) so that their opponent is indifferent between defending the pass (passing) and defending the shot (shooting). In other words, for an attacker we want to find P such that:
P * xG(Pass | Defend Pass) + (1 – P) * xG(Shot | Defend Pass) =
P * xG(Pass | Defend Shot) + (1-P) * xG(Shot | Defend Shot)
To run the math though, we need a few numbers that will help us calculate the cost-benefit for both the attacker and the defender. First, we need to know how often teams score when they shoot or pass on a 2-on-1. While the NHL doesn’t track this kind of stat, we can use data from Ryan Stimson’s passing project to estimate the shooting percentage when a team passes or shoots on a 2-on-1. Within Stimson’s data, teams that had their last pass before a shot in the offensive zone scored on 26.8% of their shots, while teams that had their last pass before a shot on a 2-on-1 outside of the offensive zone scored on just 14.2% of those shots. While these are broad estimates (there were only 374 2-on-1 shots recorded in his dataset), they should be good enough for our purposes.
Next, we need to know how often teams are successful when they chose to pass on a 2-on-1. Unfortunately, no one has tracked this data so we’ll have to pick numbers that seem reasonable. We also need to provide estimates by the defenders actions, so we’ll assume that the attacker is successful in making a pass 50% of the time when the defender chooses to play the pass, and 80% of the time when the defender chooses to play the shot.
Lastly, we need to know how often a defender will block a shot when they choose to play the shot rather than the pass. Once again, we don’t have the actual data to calculate this number, but in this case we know that defenders block around 25% of the shots that are taken during all situations in a game. We can assume that the block rate on a 2-on-1 is much lower, so let’s put it at 12.5% – again it’s a guess, but it’s a fairly low number and it should be good enough to give us a general estimate.
With all of our assumptions out of the way, we can look at the expected goals for each scenario (attacker shoot or pass, and defender play the shot or pass).
| Attacker Shoot[3] | Attacker Pass | |
| Defender Play Shot | (1 – 0.125) * 0.142 = 0.124 | 0.8 * 0.268 = 0.214 |
| Defender Play Pass | 0.142 | 0.5 * 0.268 = 0.134 |
Obviously if you’re a defender you want to minimize your expected goals against, so your best case scenario is that the attacker shoots and you play the shot. But if you’re the attacker and you know that the defender is likely to play the shot to get their best case, you’ll probably pass, since your expected goals are higher if you pass when the defender plays the shot. But if you’re a defender and you know the attacker is going to pass, you’ll play the pass. And then if you’re the attacker…well you see how you could go on for a while, right?
But, if we use the equation we had above, we can figure out the equilibrium for this problem, that is how often the attacker should shoot so that the defender doesn’t care whether they play the shot or the pass (and similarly, how often the defender should play the pass so the attacker doesn’t care whether they shoot or pass).
And as it turns out the conventional wisdom of always play the pass is *almost* right – the equilibrium for this game (based on our assumptions that we noted above) is that defenders should play the pass roughly 92% of the time and defend the shooter just 8% of the time. On the other hand, shooters should take the shot 82% of the time, while trying the pass just 18% of the time. And while these numbers are really heavily dependent on our assumptions, they do make a lot of sense – often the conventional wisdom exists because it’s right, and if you’re a forward who knows the defender is probably playing the pass, you’re likely going to opt for the shot most of the time, while occasionally taking a risk for the higher percentage tap in.
But even though the results make sense, what if our assumptions are actually wrong? The blocked shot number might not matter that much and is probably within a reasonable range given that we actually had some data to base it off of, but the pass completion rates were kind of drawn out of thin air. If these numbers are different in reality, our view of the optimal strategy for both forwards and defenders would change as well.
We can see the impact of our assumptions by looking at how the equilibrium for the attacker and defender change as we vary the pass success rates depending on defender choice. We’ll assume that the probability of a pass being successful is always higher if the defender chooses to play the shot than the pass, which is why you won’t see any data in the top left half of the graphs below.
First, let’s look at defenders – each point on the graph below represents how often the defender should play the shot, depending on the pass completion percentage when playing the shot (x-axis) and the pass completion percentage when playing the pass (y-axis).
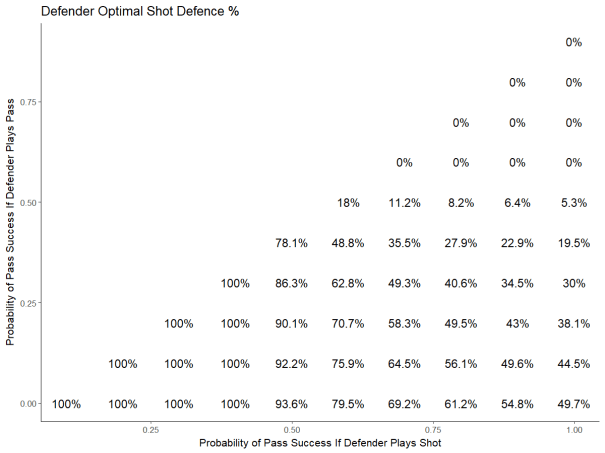
There are 3 things that stand out in this graph:
- If the pass completion percentage is low (40% or less), the defender should always play the shot – this makes a lot of sense, given that the shooting percentage on passes is roughly double the shooting percentage on shots. If you complete a pass less than half the time, then shooting becomes the more dangerous decision no matter what, and so the defender should always choose to play the shot.
- If the pass completion percentage when the defender plays the pass is high (>= 60%) the defender should always play the pass. This might feel slightly counterintuitive, but when you consider that the pass completion percentage when you play the shot is always even higher, it becomes clear that the forwards incentive would be to pass most of the time, and therefore you should want to defend against the more dangerous play.
- In the middle region, there’s a lot of variability in how often you should play the pass. While in our original example we calculated that a defender should try to take the shooter just 8% of the time, that number would be more than 3 times higher if we had decreased our estimated pass success rate on defended passes to 40%.
We can also look at what happens to the attacking player’s decision making when we change our assumptions.
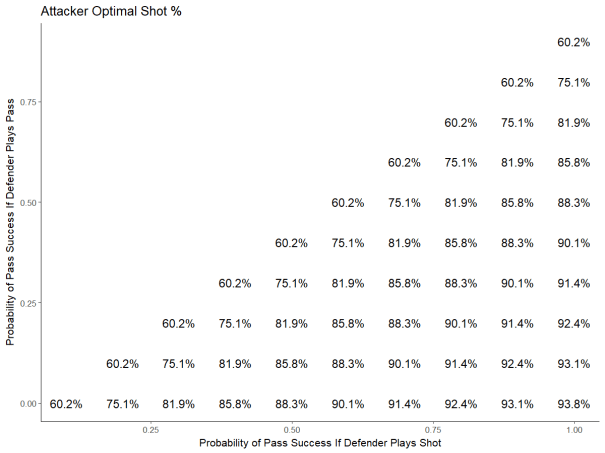
Attackers don’t show the same discrete decision regions as defenders – there’s no rates that would cause an attacker to always shoot or always pass – but we do see the same wide range of results that we saw for defencemen. While we had originally estimated that forwards should shoot 82% of the time, if we had instead assumed that attackers were successful completing a pass just 70% of the time that the defender played the shot, that equilibrium number would drop to 75%.
While it’s difficult to know where the true equilibrium lies without access to better data on player positioning and pass success rates, it’s likely that there’s no “one-size-fits-all” approach for defending an odd-man rush[4]. Even when one strategy seems to be clearly preferable to another, becoming too predictable can give your opponent an advantage and will certainly make their decision making simpler. Not having strict rules but rather broad guidelines about how to play in a given situation will ultimately lead to better results, and at the very least will help defenders avoid looking like Jake Gardiner did last night.
[1] It’s unlikely that Gardiner knew that Daley is one of the league’s most lethal defencemen on the penalty kill, sitting third amongst blueliners in shorthanded goals since 2014-15 with 2.
[2] Again, not really defying the odds since Trevor Daley may be the last player a goalie wants to face one-on-one on the power play, but how could Jake Gardiner possibly have known that.
[3] These numbers are definitely wrong, since what we observe (the 14.2%) is a blend of player’s shooting when the defender is playing the pass and when the defender is playing the shot, but without knowing how often they’re actually doing each we can’t really break it up any better.
[4] Unless Trevor Daley has the puck while shorthanded, in which case you always cover Trevor Daley.

[…] Hockey: Puck++ on The Time Value of Money and Player Valuation. Tom Tango calculates the Isolated Even-Strength Plus-Minus of Ovechkin’s career. Puck++ looks at Game Theory and Defending Against a 2-on-1. […]
[…] in Carpenter from getting closer to center ice, while blocking the shooting lane. Given recent game theory analysis, defending the shot was probably the right play. Moore still had his stick on the ice, moving […]